Tag: analog computer

turing complete

| Categories: Chinese, cs & it | Tags:

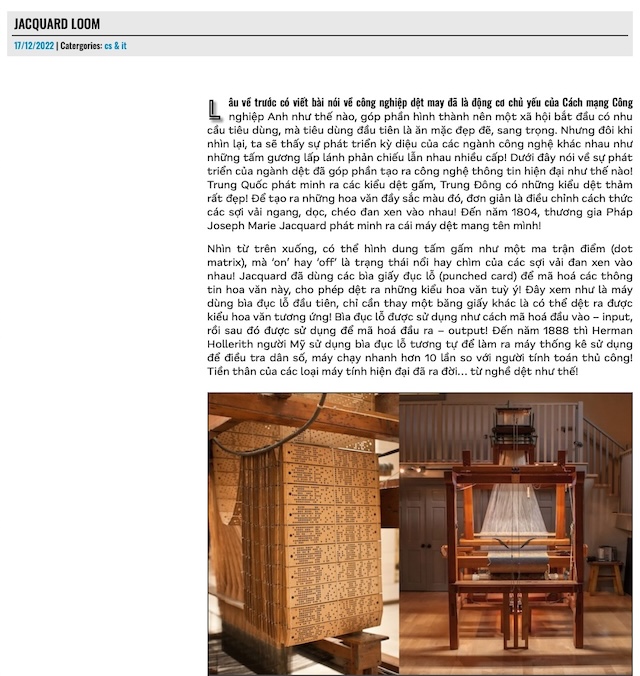
Rải rác trong nhiều năm qua, tôi đã viết khá nhiều post về “analog computer – máy tính tương tự“. Analog computer có khả năng giải quyết những bài toán cụ thể với hiệu suất (tính theo thời gian thực thi và năng lượng sử dụng) cao hơn nhiều so với Digital computer – máy tính số. Đương nhiên, analog computer không phải là toàn năng, đơn giản là vì chúng thường không “Turing complete”. Nói theo ngôn ngữ bình thường tức là chúng không đủ tổng quát để chạy một chương trình/thuật toán bất kỳ mà chỉ có thể dùng cho một số lớp bài toán cụ thể, cố định đã thiết kế từ trước mà thôi.

Mà trong ngữ cảnh A.I. ngày nay thì thường đó là các bài toán phân giải ma trận – matrix decomposition. Nên chuyện tương lai sẽ có những hệ thống lai, vừa có các thành phần analog & digital cùng một lúc là điều có thể thấy trước! Trong năm 2024, TQ đăng ký (và đã được chấp thuận) gần 1 triệu bằng phát minh sáng chế, chiếm 49% toàn cầu, nhiều hơn Mỹ đến… hơn 3 lần. Tuy các trường ĐH, các trung tâm nghiên cứu phương Tây vẫn dẫn đầu về tổng số bằng phát minh sáng chế tích lũy, nhưng chuyện Trung Quốc vượt lên và vượt xa là điều hoàn toàn có thể dự báo trước!

Theo các ước tính (số liệu chưa hoàn chỉnh và chính xác) thì TQ đã đạt mức 500 bằng phát minh sáng chế / 10 ngàn dân trong 5 năm qua. Cũng trong thời gian đó thì mức của VN ở vào khoảng 1.8 / 10 ngàn dân, đáng nói là gần 90% trong số đó do người nước ngoài sinh sống và làm việc tại VN thực hiện, số thực sự của người Việt chỉ là 0.18 / 10 ngàn dân! Và nếu nói theo tiêu chí này thì: hàm lượng chất xám của người TQ cao hơn VN nhiều ngàn lần!!! Vẫn tự cho là mình “thông minh” mà, đâu có tự luận ra được, thời gian dành hết cho các trò lưu manh, điếm lác lặt vặt mất rồi!

ball and disk integrator

| Categories: boat-related, cs & it | Tags:

Trong hình là một cái máy tính tích phân cơ khí, cơ chế hoạt động như sau: đĩa tròn quay với vận tốc không đổi, đại diện cho trục x, thường là thời gian t, đĩa quay làm quả bi tròn quay theo! Tùy theo vị trí của bi mà tốc độ quay khác nhau, nếu bi ở chính ngay tâm đĩa, thì tốc độ là 0, bi không xoay, nếu bi được di chuyển ra càng gần mép đĩa thì tốc độ quay càng nhanh hơn, nếu di chuyển ngược lại về phía bên kia đĩa thì bi sẽ quay theo chiều ngược lại. Bi xoay làm cho trục tròn nằm ngang xoay theo, nếu ta di chuyển bi qua lại dọc theo đồ thị của một hàm số f(x) thì, không quá khó để hình dung, số vòng quay tích lũy của trục chính là tích phân của hàm f(x), nói một cách đơn giản chính là diện tích phần ‘nằm bên dưới’ đường cong f(x).

Chỉ cần đếm số vòng quay của trục thì sẽ nhận được giá trị của tích phân này. Căn bản đó chỉ là một cái máy tính tích phân cơ học, nhưng ứng dụng thì quá quan trọng đến nỗi người ta cho rằng đây là thiết bị quan trọng nhất từng được chế tạo trước khi máy tính điện tử ra đời! Máy chỉ thị mục tiêu và dẫn bắn trên chiến hạm Dreadnought là sử dụng cơ chế đĩa và bi, máy tính dẫn bắn cho các loại ngư lôi trong WW2 là dạng bi và đĩa, máy quan sát ném bom – Norden bombsight cũng là dạng bi và đĩa, và vô số máy móc, thiết bị khác. Hình là máy phân tích thủy triều chế tạo bởi Sir Kelvin (William Thomson), đĩa không chuyển động tròn đều mà chuyển động hình sin, nhưng căn bản, đây chính là máy tính tích phân đầu tiên!

tidal analysis

| Categories: boat-related, cs & it | Tags:

Thủy triều được dự đoán, tính toán như thế nào? Vì có quá nhiều tham số tác động đến thủy triều, như M2 (moon) hay S2 (sun), và nhiều hành tinh khác, nên dự đoán thủy triều được bắt đầu bằng việc… thu thập, ghi chép số liệu thực nghiệm tại một cảng nào đó, số liệu này được thu thập trong nhiều năm và sau đó dùng một phép biến đổi Fourier để phân tích hàm thủy triều (số liệu) này thành tổng của các hàm lượng giác con, mỗi hàm con có dạng f(t) = A x cos(st + p), với A (amplitude) là độ lớn, biên độ dao động, s (speed) là vận tốc góc, p (phase shift) là độ lệch pha, và t là thời gian. Mỗi hàm lượng giác điều hòa con này là đại diện cho mức độ ảnh hưởng của một yếu tố riêng biệt, như mặt trời, mặt trăng, các hành tinh, etc…

Nhưng ngày xưa chưa có máy tính điện tử, người ta phân tích Fourier như thế nào? Cũng lại là dùng các máy tính cơ học, trong ảnh là máy phân tích thủy triều được chế tạo bởi Sir Kelvin (William Thomson) năm 1878, máy dài 6m. Sau khi đã phân tích dữ liệu quá khứ đã thu thập và có được các tham số thì lại nhập các tham số này vào máy dự đoán thủy triều (đã nói ở bài trước) để tính thủy triều tại một thời điểm cụ thể nào đó trong tương lai. Về máy phân tích thủy triều thì có nhiều chuyện phức tạp, nhưng về máy dự đoán thủy triều, cơ chế vận hành của nó lại khá đơn giản. Hình thứ 2 là cơ chế máy dự đoán thủy triều, hàng bánh xe trên là cố định, hàng bánh xe dưới có thể chỉnh được tốc độ, độ lớn cũng như độ lệch pha!

Chính là biểu diễn các tham số A, s và p trong công thức nói trên. Sau đó thông qua những cái “Scotch yoke” (cái này không biết phải dịch ra tiếng Việt thế nào) để biến chuyển động quay thành chuyển động tịnh tiến, kéo các ròng rọc chạy! Nguyên hệ ròng rọc chạy và kéo một sợi dây, sợi dây này kéo một cây bút trên bề mặt một băng giấy xoay tròn, vẽ thành đồ thị thay đổi lên xuống của thủy triều theo thời gian. Hàm tổng (thủy triều) được tổng hợp lại từ các hàm con đơn giản như thế! 150 năm trước người ta đã tìm cách phân tích và tổng hợp chính xác, 150 năm sau, chúng ta tổ chức giải đua ghe nhưng rút cuộc không đua được vì phải chờ đến “giờ lành” để bắt đầu thì nước triều đã rút cạn chỉ còn tới đầu gối!

July 4th

| Categories: boat-related | Tags:

Ngày 4 tháng 7 vừa qua là một ngày rất đặc biệt, trái đất ở xa mặt trời nhất trong năm, xa hơn khoảng 3% so với đường tròn lý thuyết, vì quỹ đạo của trái đất quanh mặt trời là một hình tựa ellipse có 2 tâm! Điều này dẫn đến tác động của lực hấp dẫn của mặt trời lên thủy triều giảm xuống khoảng 5%, đồng thời trăng thượng huyền cũng là giai đoạn mà tác động của lực hấp dẫn của mặt trăng giảm thêm khoảng 8% nữa… Các kênh rạch, sông ngòi ở Sài Gòn, mực nước triều xuống ở mức thấp gần như suốt ngày, nhiều nơi cạn trơ đáy! Đến cỡ cuối năm sang đầu năm mới, trái đất quay đến vị trí gần mặt trời nhất nên sẽ xuất hiện triều cường, đặc biệt khi kết hợp với trăng non! Tính toán thủy triều không phải là một việc quá đơn giản…

Nói theo nghĩa rộng thì đó là một “phương trình” vô hạn tham số, nhưng thực tế trong thủy đạc, người ta chỉ dùng vài chục tham số chính (mặt trời, mặt trăng, etc…) để tính xấp xỉ thủy triều. Hình bên dưới: máy tính cơ học, dùng để tính thủy triều, chế tạo bởi William Thomson năm 1872 ở Anh, máy có 10 tham số. Nước và những con tàu, đó là những “chỗ đứng” vô cùng đặc biệt, đứng trên boong một con tàu, dù là một chiếc kayak bé xíu, hay là một chiếc tàu hàng trăm ngàn tấn, bạn có thể thấy được rất nhiều thứ: trên thì trông thiên văn, dưới thì nhìn địa lý, rộng thì thấy thế giới, hẹp thì thấy vùng miền, xa thì nhìn khắp lịch sử, gần thì tìm hiểu khoa học kỹ thuật, cao thì thấy dân trí, mà thấp thì nhìn rõ lòng người… :)

Jacquard loom, 2

| Categories: cs & it, history | Tags: ,

Mấy năm trước, có viết một đoạn về Jacquard loom, tiền thân của các loại máy dệt tự động hóa hiện đại, dùng bìa đục lỗ (punched card) để mã hóa thông tin hoa văn trên vải dệt. Thay một cái bìa là nó sẽ dệt ra một kiểu hoa văn mới, hoàn toàn tự động. Mới nghe thì có vẻ không có liên quan gì, nhưng máy dệt Jackquard có thể được xem là “sơ tổ” của các loại máy tính hiện đại. Nói thêm một chút về số phận của Joseph Jacquard, người phát minh ra cái máy dệt này. Hôm nay, ta hãy ngồi vào cỗ máy thời gian, thời điểm là năm 1802, điểm đến là tp. Lyon nước Pháp! Allez-y, maintenant!

Jacquard cầm cố tài sản đến mức khánh kiệt để chế tạo ra cái máy dệt đi trước thời đại này! Kết quả là… các công nhân dệt sợ máy cướp hết công việc nên đã tập hợp lại, đập phá cái máy, Jacquard bị ném xuống sông, may mà không chết! Ở Đức, tình hình còn phát triển đến mức cực đoan hơn, công nhân biểu tình phản đối, bạo động tràn lan, chính quyền phải ra lệnh tử hình đối với những người phát minh ra các loại máy dệt mới để trấn an dân chúng! Nên chuyện trí tuệ nhân tạo – AI hiện đại thực ra không phải là vấn đề gì mới, chỉ là lịch sử lặp lại chính nó mà thôi!

máy tính tương tự

| Categories: cs & it | Tags: ,

Những máy tính tương tự – analog computer đang dần dần trở lại, ít nhất trong một vài lĩnh vực hẹp! Thấy các bạn thanh thiếu niên ở Anh, châu Âu toàn bắt đầu học lập trình với các mạch Arduino, Raspberry pi, etc… theo tôi đây là cách học rất hay, học một điều gì thì nên bắt đầu từ cái đơn giản, cụ thể, đừng vội biến nó thành vấn đề trừu tượng, to tát, mang tính học thuật! Nhưng như thế nào là một máy tính tương tự, ngay điều này cũng không phải lúc nào cũng dễ hình dung! Giả sử ta làm một mạch điện đơn giản chỉ có biến trở R, được áp một điện thế V! Dòng điện đi qua được hiển thị bằng đồng hồ đo là I. Vì I tương quan với V và R theo công thức: I=V/R, nên khi thay đổi V và R (xoay các núm điều khiển), ta sẽ có được kết quả I hiển thị trên đồng hồ đo, như là kết quả của phép chia V cho R.

Như thế, phép chia không được biểu diễn bằng các bít nhị phân, mà được biểu diễn bằng “vật chất”, tức là dòng điện! Các nhà giáo dục phải bỏ công suy nghĩ về những cách trình bày, chứ nếu chỉ như câu số 6, đề Toán tuyển sinh lớp 10 tp.HCM thì vẫn còn đơn giản lắm! Bắt đầu bằng những cái cụ thể, đơn giản, giữ liên hệ chặt chẽ với thế giới xung quanh, làm cho việc học trở thành sự ham thích lâu dài! Nếu không chúng ta chỉ biến học sinh trở thành những cỗ máy tụng bài chạy theo các số đo hư ảo, những vọng động nào đó trong “tâm” của những người “đóng vai” phụ huynh và thầy cô mà thôi! Muốn tụi nhỏ thực á, trước hết chúng ta phải tự biết cái gì là thực và phải có bản lĩnh để kiên định cái thực đã! Vì không làm được nên quay sang ép con trẻ chạy theo những cái “bánh” do mình “vẽ” ra!

Planimeter

| Categories: cs & it | Tags: ,

Mấy chục năm KHMT và CNTT, đôi khi tôi cảm thấy cần phải cho đi lại từ đầu, chưa đi vội về sau, đôi khi cần phải hiểu lại những điều rất rất cơ bản! Ví dụ như vẫn có nhiều người có thể đã học hết 12 năm phổ thông nhưng chưa chắc đã hiểu một “phép nhân” đơn giản!

Dưới đây là ví dụ vế Planimeter, một cái “máy” rất chi là “hấp dẫn và kích thích suy nghĩ”, máy tính “cơ học”, máy tính “analog”, dùng để tính diện tích của một hình bất kỳ, đó là thời đại trước khi máy tính, với tất cả những phần mềm CAD, CAM xuất hiện…

jacquard loom

| Categories: cs & it | Tags:

Lâu về trước có viết bài nói về công nghiệp dệt may đã là động cơ chủ yếu của Cách mạng Công nghiệp Anh như thế nào, góp phần hình thành nên một xã hội bắt đầu có nhu cầu tiêu dùng, mà tiêu dùng đầu tiên là ăn mặc đẹp đẽ, sang trọng. Nhưng đôi khi nhìn lại, ta sẽ thấy sự phát triển kỳ diệu của các ngành công nghệ khác nhau như những tấm gương lấp lánh phản chiếu lẫn nhau nhiều cấp! Dưới đây nói về sự phát triển của ngành dệt đã góp phần tạo ra công nghệ thông tin hiện đại như thế nào! Trung Quốc phát minh ra các kiểu dệt gấm, Trung Đông có những kiểu dệt thảm rất đẹp! Để tạo ra những hoa văn đầy sắc màu đó, đơn giản là điều chỉnh cách thức các sợi vải ngang, dọc, chéo đan xen vào nhau! Đến năm 1804, thương gia Pháp Joseph Marie Jacquard phát minh ra cái máy dệt mang tên mình!

Nhìn từ trên xuống, có thể hình dung tấm gấm như một ma trận điểm (dot matrix), mà ‘on’ hay ‘off’ là trạng thái nổi hay chìm của các sợi vải đan xen vào nhau! Jacquard đã dùng các bìa giấy đục lỗ (punched card) để mã hoá các thông tin hoa văn này, cho phép dệt ra những kiểu hoa văn tuỳ ý! Đây xem như là máy dùng bìa đục lỗ đầu tiên, chỉ cần thay một băng giấy khác là có thể dệt ra được kiểu hoa văn tương ứng! Bìa đục lỗ được sử dụng như cách mã hoá đầu vào – input, rồi sau đó được sử dụng để mã hoá đầu ra – output! Đến năm 1888 thì Herman Hollerith người Mỹ sử dụng bìa đục lỗ tương tự để làm ra máy thống kê sử dụng để điều tra dân số, máy chạy nhanh hơn 10 lần so với người tính toán thủ công! Tiền thân của các loại máy tính hiện đại đã ra đời… từ nghề dệt như thế!

phương trình vi phân

| Categories: Russian | Tags: , ,

Máy tính ống nước, dùng để giải phương trình vi phân, phát minh bởi Vladimir Lukyanov ở Liên Xô năm 1936, được dùng mãi cho đến cuối những năm 80, dùng để tính toán xây dựng vô số công trình kênh đào, hầm mỏ, đường sắt, và nhiều bài toán thực tế khác! Nguyên tắc khá đơn giản, là tập hợp các ống thuỷ tinh chứa nước thông với một ống chính (biểu diễn hàm ẩn). Các ống này có thể cố định, hoặc di động, thông với ống chính qua những valve lưu lượng có thể điều chỉnh được! Nước được đổ vào các ống theo những mức định trước, sau đó họ mở đồng loạt các van và di chuyển các ống di động, mực nước trong ống chính biến thiên và được ghi lại trên một cuộn giấy xoay, đó chính là nghiệm phương trình!

Đến ngày nay, chắc chúng ta không ai có thể nhớ nổi phương trình vi phân là cái gì, bây giờ không nhớ và tôi dám chắc là đa số cũng như tôi ngày xưa, cũng loay hoay thời gian dài mà vẫn không hiểu: phương trình vi phân nó thực sự là cái gì!? Chính là nhờ nhìn vào cái máy tính analog này mà thực ra mọi chuyện trở nên rõ ràng: mây bay, nước chảy, gió thổi chính là phương trình vi phân! Và việc học toán ở VN không gây được hiệu ứng tích cực, đơn giản vì các ông ấy loay hoay với các công thức, biểu tượng, các ký tự chết mà quên mất rằng bản chất vấn đề nằm trong những vận động thực của cuộc sống, phải đưa thật nhiều ví dụ ứng dụng thực tế, ví dụ về tính tương tự trong thế giới thực thì học sinh mới nắm được nội hàm của vấn đề!

Nói về phương pháp sư phạm, học sinh cấp 1 khó hình dung hệ đếm, nhưng nói với nó 3, 5 cây kẹo, là sẽ hiểu! Học sinh cấp 2 nói về phân số rất khó hiểu, nhưng bảo cầm can đi mua 3 lít rưỡi dầu là nó hiểu! Học sinh cấp 3 có thể không hiểu về vi tích phân, nhưng biểu diễn diện tích hình, thể tích khối là nó sẽ hiểu! Sinh viên ĐH có thể không hiểu chuỗi số, nhưng đưa ví dụ về mortgage calculator – vay nợ và tính lời, gộp vốn và gộp lãi là chúng nó sẽ hiểu! Toán cấp 3 là tính vận tốc rơi tự do của vật, bỏ qua sức cản không khí! Toán ĐH là tính tốc độ rơi tự do của vật, kèm theo sức cản không khí (chính là phương trình vi phân). Toán sau ĐH là tính sức cản không khí ở những tầng khác nhau của khí quyển, chính là điều khiển tên lửa, cứ phải trực quan cụ thể như thế mới dễ hiểu!

Cũng như môn Văn giờ gọi là “Ngữ văn” vậy (học theo TQ), là cách gọi chính xác, học sinh cấp 2, 3 thì chưa thể hiểu văn học nghiêm chỉnh, làm sao chúng nó hiểu được chiều sâu của “Chiến tranh và hoà bình”, chẳng qua là mượn một số bài “Văn” để học về ngôn ngữ, và thông qua kỹ năng ngôn ngữ để tiếp cận “Văn học”. Cũng tương tự như vậy cho các môn khác, dạy theo kiểu trừu tượng, toàn công thức chết hại vô cùng, không những học sinh không hiểu nó đang học cái gì, mà còn làm mất đi hứng thú với môn học. Chuyện này vì một vài lần đi làm gia sư (bất đắc dĩ) nên tôi hiểu rất rõ, đám nhóc giờ chúng nó chỉ tụng công thức, vì “cô bảo thế, như cô mới đúng”, chứ chúng nó hoàn toàn không có hứng thú với chuyện học, không có sự tò mò tìm hiểu về thế giới xung quanh!

analog computers

| Categories: cs & it, Russian | Tags: , ,

Một chủ đề ưa thích của tôi là lịch sử Khoa học Kỹ thuật. Lên Đại học, tiếp xúc với các khái niệm automata, tự động hoá và điều khiển, tôi được học chung về các nguyên tắc đầu vào và đầu ra của các hệ thống máy tính điện tử. Tất cả các tín hiệu “in và out” (sensor, control, actuator…) được “lượng hoá” từ tín hiệu analog thành digital, vì máy tính hoạt động trên nguyên tắc tín hiệu số, dĩ nhiên có một số bộ chuyển đổi AD, DA đâu đó. Nhưng mãi lâu về sau, tôi mới được biết đến cái gọi là “analog computer”, ngược hẳn với “digital computer”, đó là những “máy tính tương tự”, hoạt động trên các “tín hiệu tương tự”, sử dụng những nguyên tắc cơ, điện, quang… Một ví dụ “kinh khủng” nhất cho các “analog computer” là các “máy tính” sử dụng trong điều khiển tàu vũ trụ của Liên Xô, mở ra bên trong thấy toàn các bánh xe cơ giới!

Một sự thật làm tôi há hốc mồm vì kinh ngạc! Tàu con thoi Soyuz được phóng lên vũ trụ và hạ cánh xuống mặt đất, được tự động hoá từ A đến Z, không cần người điều khiển, sử dụng những bánh xe, cánh tay đòn hoàn toàn cơ giới như thế. Trong khi “Tàu con thoi – space shuttle” của Mỹ, sử dụng “digital computer” hẳn hoi – hiện đại hơn Liên Xô cả một thế hệ, nhưng không thể tự động hoá hoàn toàn, phải có người điều khiển! Các hình dưới đây, bảng điều khiển tàu vũ trụ Liên Xô, một quả địa cầu được xoay bằng các trục và bánh xe, để chỉ cho phi công biết con tàu đang ở đâu so với mặt đất! Mở ra bên trong trông như một cái đồng hồ, một kỳ quan thực sự về cơ khí phức tạp! Phải mất rất lâu ta mới hiểu ra rằng, có nhiều hơn một cách để làm “chuyện ấy”, và những “cách khác” ấy đôi khi rất “dị” so với “quan điểm thông thường”!