 enoit Mandelbrot xuất bản một bài báo trên tạp chí Science năm 1967, nhan đề:
enoit Mandelbrot xuất bản một bài báo trên tạp chí Science năm 1967, nhan đề: Đường bờ biển của nước Anh dài bao nhiêu?
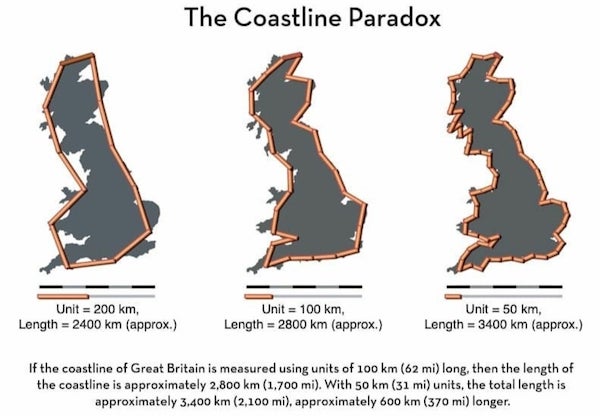
Giả sử ta dùng một cây thước dài 1 km để đo đường bờ biển, cộng lại với nhau thì được chiều dài ‘x’ km. Nhưng nếu dùng một cây thước khác, có chiều dài ví dụ như 100 m để đo thì lại được một chiều dài khác lớn hơn, ‘y’ km. Đơn giản vì cây thước 1 km là một xấp xỉ rất “thô”, ở giữa khoảng cách 1km đó, đường bờ biển không phải là một đoạn thẳng. Dễ dàng nhận thấy rằng, nếu dùng cây thước càng ngắn, thì chiều dài đo được càng tăng, và nếu chiều dài cây thước tiến dần về 0 thì chiều dài đường bờ biển tiến dần về vô hạn. Đó gọi là “nghịch lý đường bờ biển – coastline paradox”, và cũng từ đó (1967) chính thức xuất hiện một nhánh toán học mới, gọi là hình học fractal, nghiên cứu một loại đối tượng đặc biệt, ví như ở đây là bản đồ nước Anh, một đối tượng hình học có diện tích hữu hạn, nhưng chu vi… vô hạn! Đây là chủ đề yêu thích của tôi những năm cấp 3 và Đại học…
Vì nó liên quan trực tiếp tới đồ hoạ máy tính (computer graphics). Gọi là “Nghịch lý – paradox” vì nó đi ngược lại với “trực quan” của chúng ta, qua đó nói lên rằng, những gì chúng ta suy nghĩ bằng ngôn từ, đôi khi chỉ là sự lừa dối, một sự lừa dối khó nhận ra vì suốt bao nhiêu năm, cách suy nghĩ của chúng ta bị đóng trong một cái khuôn máy móc! Một câu hỏi tưởng chừng ngây ngô nhưng trả lời không hề đơn giản! Riêng về đường bờ biển VN, nếu đo bằng phương pháp VN thì nó dài khoảng 2400 km, nếu đo bằng cách của Mỹ thì nó dài khoảng 3400 km, còn nếu đo bằng “toán” thì nó… vô hạn! Có điều gì rất “Phật giáo” trong phép đo này, chiều dài của một đối tượng hình học không phải là hằng số, không phụ thuộc vào “các định luật vật lý hiển nhiên”, mà ngược lại, nó lại phụ thuộc vào cách chúng ta đo nó! Nói nôm na, phiên phiến là… “tâm” nó tới đâu thì “tầm” (chiều dài đối tượng) tới đó. Chiều dài của một đối tượng hình học Euclide đơn giản đôi khi nằm ngoài “nhận thức thông thường” của con người! 😀